Gummibänder, Federn und andere Elastizitäten

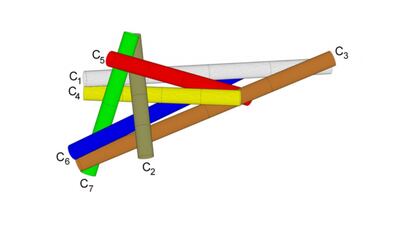
Die 6 unendlich langen Zigaretten von letzter Woche , die so in Kontakt gebracht werden können, dass jede alle anderen berührt, können verbessert werden: In der Abbildung sehen wir eine Lösung mit 7 Zigaretten, die zudem nicht eindeutig ist (können Sie eine andere finden?). Einige Kontakte sind offensichtlich, andere jedoch weniger. Wie können wir beispielsweise sicher sein, dass die Zigarette C5 die C6 berührt?

Bei der Frage zum Gummiband handelte es sich um eine Fangfrage : Würde sich das Volumen (oder anders gesagt die Dichte) des Gummibands nicht ändern, wäre seine Fläche bei einer Halbierung des Durchmessers viermal kleiner und müsste daher auch viermal so lang sein, also vier Meter. Würde der Gummi jedoch beim Dehnen sein Volumen nicht verringern, wäre er nicht elastisch, sondern wie Kaugummi und würde beim Loslassen nicht seine ursprüngliche Form wiedererlangen (und daher gäbe es keine Poissonzahl). Wenn ein Gummiband gedehnt wird, dehnen sich die Polymere (sehr lange Moleküle), aus denen es besteht und die in einem Zickzackmuster verheddert sind, aus, was zu einer Volumenreduzierung führt. Beim Loslassen des Gummis nehmen die Polymere aufgrund der Strukturkräfte der langen Moleküle wieder ihre ursprüngliche Form an. In gewisser Weise ist es so, als bestünde das Gummiband aus einer unendlichen Zahl mikroskopischer (oder besser gesagt mikrophysikalischer) Federn, so vielen wie es Moleküle gibt.

Ein widerstandsfähiges Board

Und wenn wir schon von Elastizität sprechen: Unser Carrollian Board von vor ein paar Wochen war vielleicht gar nicht so verrückt, wie es zunächst schien, sondern hat einfach einige Konzepte auf eine etwas elastischere Art und Weise verwendet. Daher ist die Gleichheit 180 = 90 + 30 möglicherweise einfach unvollständig, und + 60 fehlt, um die Beziehung zwischen den Winkeln eines rechtwinkligen Dreiecks zu vervollständigen, das die Hälfte eines gleichseitigen Dreiecks ist.

Andererseits beträgt die Winkelsumme eines Dreiecks nur in der euklidischen Ebene 180º. Auf der Erdoberfläche lässt sich leicht ein Dreieck bestimmen, dessen Winkel insgesamt 270º betragen: Ein Scheitelpunkt kann der Nordpol (oder der Südpol) sein und die beiden anderen jeweils die Städte Quito (Ecuador) und Libreville (Gabun), die beide auf dem geografischen Äquator liegen und etwa 10.000 km voneinander entfernt sind.

Was das rechtwinklige Dreieck betrifft, das teilweise durch den Kopf der jungen Blondine verdeckt wird, können wir, wenn wir die 180 darin ignorieren, davon ausgehen, dass der verborgene Wert des rechten Winkels 70º beträgt. außer dass es sich nicht um Sexagesimalgrade handelt: Die ursprünglichen jungen Frauen im Bild teilen den Umfang in 280 Einheitsbögen statt der üblichen 360.

Und wie Benedicto Torres anmerkt, kann „Poisson“ kursiv gedruckt sein, weil die Rechtschreibprüfung es als Fremdwort betrachtet hat, da es auf Französisch „Fisch“ bedeutet.

Abschließend und passend zur Beziehung zwischen Gummibändern und Federn ein Vorschlag unseres regelmäßigen Kommentators Francisco Montesinos:

Mir fällt dazu folgendes gekochtes Gericht ein. Nehmen wir eine Feder mit der Höhe lyn und Windungen an, die eine zylindrische Helix oder Spirale mit dem Radius r bilden. Als nächstes strecken wir es an einem Ende und halten das andere Ende still, bis sich seine Höhe verdoppelt hat. Die Frage ist: Wie groß wird der Radius der neuen zylindrischen Spirale sein, wenn man von einer gleichmäßigen Verformung ausgeht?

Außerdem: Wie lang ist die abgewickelte Feder?