Trucvragen

Geen enkele lezer wilde aantonen dat de 7 "oneindige" sigaretten van vorige week volledig met elkaar in contact staan ​​- ze staan ​​allemaal met elkaar in verbinding - en hij heeft ook geen andere oplossing aangedragen dan de gepresenteerde. Hier is er nog één:

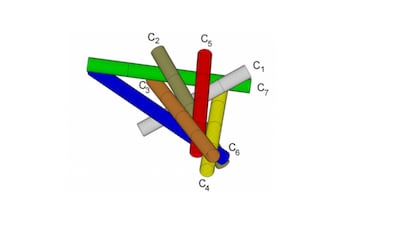
Opnieuw rijst de vraag of sommige contacten voor de hand liggen en andere minder. Hoe kunnen we bijvoorbeeld bewijzen dat de sigaretten C1 en C2 elkaar raken?

Betreffende de uitgerekte veer , is dit wat Francisco Montesinos opmerkt: "Als de straal van de windingen r constant blijft tijdens de verlenging vanwege een grote weerstand tegen de kromming van de veer, ontstaat er een tegenstrijdigheid, want als de spoed van de vervormde spiraal py is en als we de veer met een enkele winding beschouwen, zal de lengte √[(2pi.r)^2+p^2] zijn en niet (2pi.r) zoals men zou denken. Het kan terecht worden betoogd dat deze laatste r een andere r' is dan de vorige r, maar dan moeten we verduidelijken dat de straal die constant kan blijven tijdens de verlenging die van het cilindrische omhulsel van de veer is, niet die van de winding."

Rechtvaardigheid en wiskunde

Verwijzingen naar de ratio van Poisson hebben de afgelopen weken geleid tot een aantal opmerkingen over het werk van de Franse wiskundige over de toepassing van kansrekening bij het beoordelen van gerechtelijke fouten. In 1837 publiceerde Simon-Denis Poisson een essay getiteld Recherches sur la probabilité des jugements en matière criminelle et en matière civile (Onderzoek naar de waarschijnlijkheid van processen in strafzaken en burgerlijke zaken). Dit was niet de eerste poging om de calculus van waarschijnlijkheid toe te passen op de evaluatie van juridische procedures: de markies de Condorcet had in 1785 zijn Essay over de toepassing van analyse op de waarschijnlijkheid van beslissingen gegeven aan de pluraliteit van stemmen gepubliceerd, en Pierre-Simon Laplace had in zijn Filosofisch essay over waarschijnlijkheid (1814) ook geprobeerd de waarschijnlijkheid te berekenen dat het oordeel dat in een rechtszaak werd gewezen, juist zou zijn. De belangrijkste bijdrage van Poisson was dat hij beschikbare statistische gegevens en de wet van de grote aantallen in zijn analyses introduceerde om de geschatte frequentie van een gebeurtenis (bijvoorbeeld een foutieve zin) in een bepaalde tijdsperiode te bepalen. Zijn werk werd niet goed ontvangen, noch op juridisch gebied noch op wetenschappelijk gebied, hoewel het uiteindelijk zijn opmerkelijke methodologische interesse zou onthullen. Maar dat is weer een ander artikel.

Vragen en obstakels

De afgelopen weken hebben we een aantal voorbeelden gezien van 'gekookte' raadsels en strikvragen. Dat lijkt een goed excuus om er een paar te suggereren (en misschien zijn sommige ervan ook kookbaar). Hoewel het simpelweg waarschuwen dat vragen “lastig” zijn hun effectiviteit vermindert, moet je toch oppassen dat je niet op een van de volgende dingen stuit:

1. Hoeveel maanden hebben in vier opeenvolgende jaren 31 dagen, hoeveel 30 en hoeveel 28?

2. Is een vraag waarvan je het enige mogelijke antwoord al weet, altijd overbodig?

3. Wat was de hoogste berg ter wereld voordat we wisten dat het Mount Everest was?

4. Waarom slapen de meeste honden in januari meer uren dan in februari?

5. Welk dier jaagt op muizen, miauwt en krabt, maar is geen kat?

6. Wat gebeurt er als een onweerstaanbare kracht botst met een onbeweeglijk object? (Een merkwaardig verhaal: ik werd voor het eerst met deze vraag geconfronteerd in mijn kindertijd, in een stripboek waarin Superman door de tijd reist en zichzelf tegenkomt.)