Mapa-múndi de Leonardo

A área do triângulo de Reuleaux (R) da semana passada é igual à do triângulo equilátero de lado 1 (T) mais três vezes a área do segmento circular (S) em cada lado:

R = T + 3S, onde S é o setor circular menos o triângulo:

S = π/6 – T, então

R = T + 3(π/6 – T) = π/2 – 2T

T = √3/4

R = (π - √3)/2

Alguns leitores apontaram que também existem moedas com o formato de polígonos de Reuleaux. A mais conhecida é, sem dúvida, a moeda britânica de 50 pence, que tem o formato de um heptágono de Reuleaux.

A resposta à pergunta da semana passada sobre se podem existir polígonos de Reuleaux (isto é, polígonos de largura constante) construídos a partir de polígonos irregulares ou polígonos com um número par de lados, é afirmativa; mas, neste caso, os arcos do polígono resultante não serão todos iguais nem terão a mesma curvatura.

Um dos aspectos menos conhecidos, mas não menos importantes, da obra de Leonardo da Vinci é sua contribuição para a cartografia. Em sua coletânea, o Codex Atlanticus , guardado na Biblioteca Ambrosiana em Milão, há um manuscrito de 1508 no qual Leonardo analisa os vários tipos de projeções cartográficas conhecidas na época, como a projeção cônica plana de Ptolomeu e o planisfério de Contarini-Rosselli, e introduz uma nova. Essa nova projeção consiste em dividir o globo em oito octantes e, em seguida, achatá-los em triângulos de Reuleaux. Seria essa uma escolha arbitrária ou puramente estética, ou o achatamento de um octante de uma esfera produz necessariamente um triângulo de Reuleaux?

Leonardo agrupou os quatro octantes de cada hemisfério formando uma espécie de trevo de quatro folhas, com os polos nos respectivos centros de cada trevo, dando origem ao que é conhecido como o "Mapa Mundi de Leonardo", embora sua autoria não seja certa (alguns acreditam que foi desenhado posteriormente por um de seus assistentes); mas o que está solidamente demonstrado é que o gênio renascentista foi o primeiro a propor a projeção em octantes e seu agrupamento em dois trevos de quatro folhas, como atestam, entre outras coisas, um esboço do manuscrito de 1508 mencionado anteriormente e incluído no Codex Atlanticus .

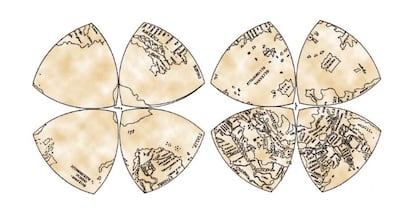
É importante notar que a projeção octante não é nem conforme nem equivalente em área. Em cartografia, uma projeção conforme preserva os ângulos (ou pelo menos a maioria deles), como as projeções de Mercator ou estereográficas, enquanto uma projeção equivalente em área preserva as proporções das áreas de diferentes países ou outras regiões geográficas representadas. Outras características que podem ser desejáveis ​​de preservar, dependendo do tipo de mapa que está sendo criado, são o formato de diferentes áreas geográficas, distâncias, direções, etc., e às vezes preservar uma dessas variáveis ​​significa distorcer outras. Uma projeção cartográfica pode ser simultaneamente conforme e equivalente em área? Como?

E, para concluir, dirijo-me aos meus perspicazes leitores a uma questão que, embora possa parecer botânica, é puramente lógica: Existem trevos de quatro folhas?